Egyptian Slides

General Slides

Maps:

Timelines: (second shows interactions)

Sketch of Egyptian History

Traditionally divided into three "Kingdoms" (with 30 or 31 dynasties) .
Between the Kingdoms were periods of chaos, foreign invaders, and/or a breakdown of unified authority.

1. Old Kingdom

Monuments

Old Kingdom known for its pyramids and other monuments. (Building during flooding theory.)
Famous examples:
1. The Great Pyramids of Giza (largest for Khufu).
2. The nearby Sphinx.

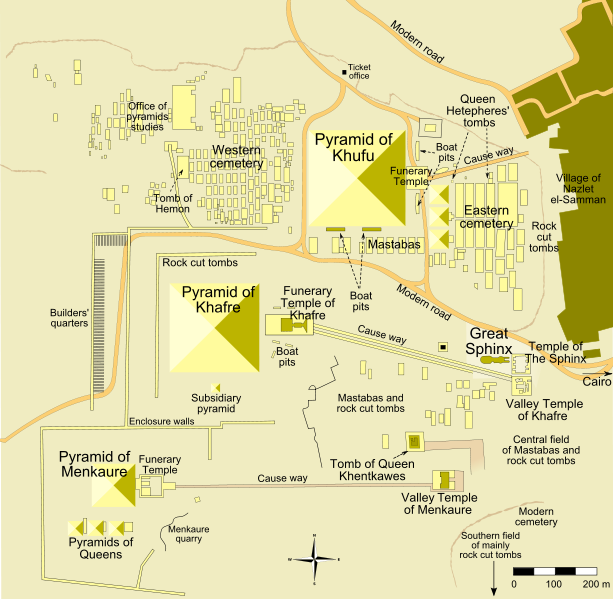
Note: These monuments are from the Fourth dynasty: c. 2575 - c. 2465 BC
Note: Another name for Khufu is "Cheops"

Unification

Old Kingdom starts with the unification of Two Kingdoms (around 3100 BC):
Upper Egypt (White Crown) is the southern narrow part
Lower Egypt (Red Crown) is the northern delta region.
Capital in Memphis at the boundary between Upper and Lower Egypt.

Cultural Background

1. Egyptian writings , called hieroglyphics, developed just before the unification (ca. 3100 BC).

2. Copper working.
3. Ruled by Pharaoh, the living embodiment of the god Horus.

Note: this is Khafri and Horus. Khafri successor to Khufu. Second largest pyramid, head of the Sphinx.

2. Middle Kingdom

Both of the main mathematical papyri represent the mathematics from this time.

Cultural Background

Known for: organization, trade, culture.
Perhaps less centralized than Old Kingdom.
Cult of Osiris. Amon-Re popular.
Refined sculpture and other art.

New capital Thebes (near modern Luxor)

End of Middle Kingdom

Ended with the Hyksos invader (about 1630 BC).
Hyksos rule lasted over 100 years.
They brought knowledge of horses, chariots, composite bows.
Some of the Hyksos might have come from Palestine.
Ahmes, the scribe lived during this period.

3. New Kingdom:

Egyptian empire well beyond the Nile.
Exodus in the Bible.
Thebes again the capital much of the time (Valley of the Kings).
Also a know for its art

Several "Celebrities" date from this time:
1. Hatshepsut (most successful female pharaoh)

2. Akenaten (monotheism, god named Aten),

3. Nefertiti (wife of Akenaten, Female Pharoah?)
(Altes Museum, Berlin)
4. Tutankhamun (King Tut, the boy king)

5. Ramses II (Most powerful pharaoh)

Monuments: The valley of the Kings, temple of Ramses II, etc.

4. Later Egypt

Often not independent, at times swallowed up by
Nubian Kingdom (from the South)
Assyrian Empire (from the East)
Persian Empire
Alexander the Great

Some periods of independence

Last major ancient Egyptian "Celebrity"
Cleopatra (69 to 30 BC) the last Ptolomaic ruler

Had a Romance with Julius Caesar but married Mark Antony
After that, Egypt was part of the Roman Empire

bust of Cleopatra (Altes Museum, Berlin)

Anthony and Cleopatra, Lawrence Alma-Tadema (1885)

The Death of Cleopatra, Reginald Arthur (1892):

Other images.

Culture

Language and Writing

Scribes managed the society, did most of the writing.
Duties: Converting currency (no one currency). Taxes. Boundaries. Inheritance. Estimations.
Revered the god Thoth.

Old Kingdom sculpture of a Scribe. The Ibex headed Thoth.

The Egyptian language: not Semitic, but related to Semitic languages (Hebrew, Arabic, Aramaic, Akkadian, etc.).
(Afterwards the Egyptian language evolved into Coptic. Many Egyptians spoke Greek during the Helenistic and Roman eras. Later Arabic became the main language of Egypt.)

Three ancient types of writing: hieroglyphics, hieratic, demotic.

1. Earliest form: Hieroglyphics ("sacred carvings"). Often finely carved, but sometimes quickly written as "cursive hieroglyphics".

2. Hieratic. Use of papyrus led to the hieratic form of writing.
Hieratic means "priestly", but it was used by scribes as well.
(Papyrus was once plentiful in Egypt. Not today: climate change)

3. The third form, Demotic ("popular"), was developed: around 600 or 650 B.C.
But priests still continued to use hieratic (hence the name).

The Nile

Longest river in the world (5588 km, 3473 m, Lake Victoria to Mediterranean).
Annual predictable flooding (before Aswan Dam) depositing Nutrients.
Provided transportation, irrigation, communication.

The flooding of the Nile was predictable.
When the bright star Sirius rose just before the sun (around the end of June),
The Egyptians knew flooding was on the way.
Flooding distributed nutrients, making the soil fertile.

Religion

Horus (falcon god-king),

Ra (or Re, the sun god, also associated with Amun as Amun-Ra popular in the Middle and New Kingdoms),

Ptah and Atum (creator gods),

Isis (mother of Horus, goddess of magic),

Osiris (ruler of underworld, fertility god, husband-brother of Isis, father of Horus).

Thoth (god of knowlege, wisdom, writing, and mathematics often ibis-headed).

Anubis (guide and guardian of the dead).

Several other gods and goddesses.

Egyptology

The Rosetta Stone led to the decipherment of hieroglyphics.
Before then our knowledge of Ancient Egypt was limited: based on the Bible and information provided by the Greeks. Herodotus etc.

Modern Egyptology began with the discovery of the Rosetta Stone (1799).
Napoleonic invasion of Egypt (1798): scholars came along.
Discovered in Rashid (called Rosetta in England), near Alexandria.

Now in the British museum (where you can buy a replica).
Black basalt. 762 kg. 1.18 meters high. 77 cm wide. 3 cm thick.
3 parallel texts: Hieroglyphics, Demotic (cursive), ancient Greek.
It is a royal decree from 196 BC written three times.

The Frenchman Jean-François Champollion deciphered Egyptian (building on the work of others.
Started age 18 around 1808. Published solution in 1822.
The famous scientist Thomas Young also helped in the decipherment.

To put the dates in perspective:
Tutankhamen's tomb discovered in 1922.
Undisturbed tomb: rare find due to thousands of years of looters

Jean-François Champollion (1790 -1832) and Thomas Young (1773 - 1829).

Mathematics

Numbers

Based on powers of 10, with each power being given its own hieroglyphic character.
Colorful site with hieroglyphic numbers.
Mac Tutor pictures of both hieroglyphic and hieratic numbers.

Old Kingdom has these numbers, but no preserved mathematics.
To see mathematics we have to wait until the Middle Kingdom.

Mathematics Texts

We only have a few with actually mathematics.
(Many sources with numbers.)
Two major sources.
Several minor sources.

Types of problems

Word problems: grain, wages, beer, slope of pyramids.
Egyptian multiplication and division using doubling.
Use of unit fractions.
Solving simple linear equations.
Slope problems involving Pyramids.
Area problems involving circle, rectangles and triangles.
Volumes of cylinders. (Truncated pyramid in Moscow Papyrus)
Solutions using the technique of false position.
Square roots.
Progressions.

1. Rhind (or Ahmes) Mathematical Papyrus

Rhind Mathematical Papyrus:
Scroll with dimensions 13 inches high, 18 feet long.
In hieratic writing.

A. Henry Rhind: a lawyer from Scotland.
Came to Egypt for reasons of health (mild climate)
Purchased RMP and EMLR at Luxor in 1858
Both came from ruins of Rameseum at Thebes
In 1864 both writings went to British Museum.
[Source: Gillings page 89]
(pBM 10057 and 10058)
(A few fragments not bought by Rhind went to the Brooklyn museum).

Papyrus dates from 1650 BC.
Starts with a unit fraction table.
Has 85 problems.
Written in the hieratic script.
From an earlier source in the middle kingdom (2000 to 1800 BC).

Scribe's name: Ahmes (or Ahmose in the following quote).
His is the oldest preserved name in the history of mathematics!
(Remember: Egyptian writing did not specify vowels, so
Ahmes and Ahmose are different interpretations of the same spelling.)

Here is Ahmes's introduction (Chase's translation):

Acurate reckoning. The entrance into the knowledge of all existing things and all obscure secrets. This book was copied in the year 33, in the 4th month of the inundation season, under the majesty of the king of Upper and Lower Egypt, A-user-Re, endowed with life, in likeness to writings of old made in the name of the king of Upper and Lower Egypt, Ne-me-et-Re. It is the scribe Ahmose who copies this writing.

The ruler A-user-Re mentioned above probably was the sixth Hyksos ruler. The pharaoh Ne-me-et-Re is also known as Nemare, or Ammenemes III who lived approximately 1842 to 1797 BC during the Middle Kingdom (according to Gardiner).

2. Moscow Mathematical Papyrus

Dimensions: 3 inch wide, 18 ft. long
Discovered in 1893 by a Russian collector
Now in the Moscow Museum of Fine Arts (catalog number 4576).

Has 25 problems
Dates from 1850 BC
Most famous is Problem 14: volume of the truncated pyramid,

Problem 14, and a possible explanation.

Challenge: try to derive the Egyptian formula by algebraically manipulating P - Q
where P is the modern algebraic formula for the volume of a pyramid, and Q is the volume of the part removed.

3. Minor Sources

Unfortunately, very little of Egyptian mathematics has survived the ravages of time. Here is a list of other sources.

1. EMLR Egyptian Mathematical Leather Roll. (Also purchased by Henry Rhind).

2. Rollin papyrus, (1350 BC bread accounts)
3. Harris papyrus (1167 BC)
4. KP. Kahun Papyrus. (British Museum. W. M. F. Petrie at Kahun in 1889 has 6 mathematical fragments)
5. RP. Reisner Papyri. (Museum of Fine Arts, Boston. 38.2062).
6. BP. Berlin Papyrus. (In Staatliche Museen, Berlin 6619)
7. AMP. Akhmim Papyrus. (Cairo Museum. Papyrus number 10758)
8. MichP. Michigan Papyri. (University of Michigan, Ann Arbor).
9. Later Greek era texts.
10. Greek tradition. (Aristotle. Herodotus. etc.)

The EMLR (Egyptian Mathematical Leather Roll) is interesting based on its material.
On costly leather in hieratic writing
Not even able to be unrolled until 1927: too brittle
A chemical treatment of leather was used
10 by 17 (inches).
26 sums of unit fractions (done twice).
One error (line 17 has 28 instead of 26)

Unit Fraction Technique

The key to using unit fractions is a way to convert two times 1/n into unit fractions.
My table .

Sample Questions:
1. explain how to use the equation 2/3=1/2+1/6 to find formulas for 2/n where n is any multiple of 3.
2. What do you do to find 3/n or 4/n using the 2/n table.
3. What do you do to find 2/n if n is even?
4. Show that if n=2m+1 is odd then 2/n can be written as 1/(m+1) + 1/n(m+1). Use modern algebra to justify the formula.

Egyptian Pi

Area of circle was (approximated by) what we can call the "8/9 square":
(replace the given circle by the square with length equal to 8/9 of the diameter)

Possible Derivation

Of course, the Egyptians did not have our concept of pi.