Example: Epic of Gilgamesh, the world's first known Epic, was best preserved in the Akkadian language.
But the story is Sumerian in origin.

Not an ideal term: some mathematics predates
the founding of the city of Babylon.
But most of the mathematical tablets have been found
in or near Babylon.
"Mesopotamian" (Greek meso + potamos "river").
Modern day Iraq.
Mesopotamian civilization is based on two rivers: Tigris and Eurphrates.
Flooding less predictable than the Nile.
More draining and cooperation needed for farming.
Rivers changed course over time.
More turbulent history than Egypt.
Most buildings: mud brick (not wood or stone).
British Museum educational website on Mesopotamia.











Some Akkadians, like the famous Sargon, ruled an empire over all of southern Mesopotamia (for 56 years ca. 2300 BC).

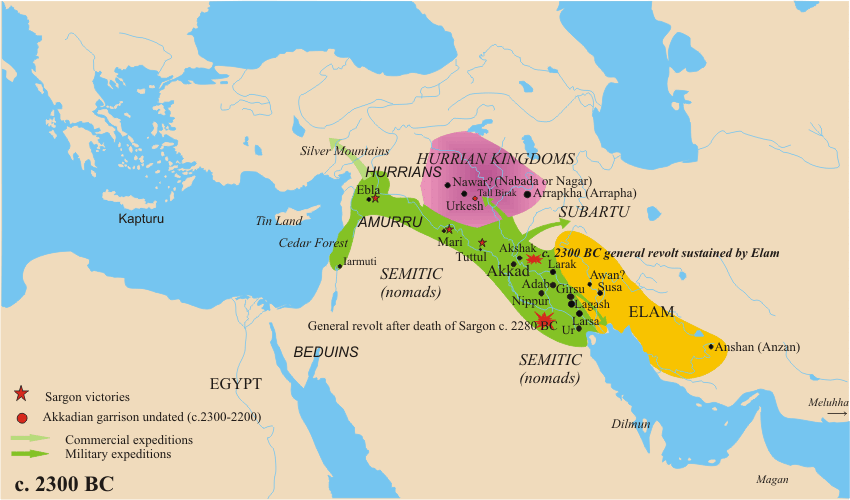 Akkadian was a Semitic language
(related to Hebrew, Arabic, and Aramaic).
Akkadian was a Semitic language
(related to Hebrew, Arabic, and Aramaic).
Akkadians adopted the Sumerian culture.
Example: Epic of Gilgamesh, the world's first known Epic,
was best preserved in the Akkadian language.
But the story is Sumerian in origin.

The last major Sumerian dynasty (following Sargon's Akkadian dynasty)
was called Ur III.
Ur is famous for its ziggurat.
Other Sumerian cities had them as well.
Not a pyramid. Not a tomb, but a temple platform.


Note: The word ziggurat ("zig gah rat") is derived from the Akkadian word ziqqurratu.
It entered English in 1877.
Some mathematical tablets date from this period (c. 2100 BC).
Most date from the next period.
Famous ruler Hammurabi
(c. 1792 - c. 1750 BC)
Sixth King of Old Babylonian Period.
Hammurabi is famous for his empire and his (harsh)
Code of Laws.
The inscription of 282 laws was found in Susa (Iran) 200 miles away. Perhaps
a war trophy.
Hammurabi ruled much of Mesopotamia (now called Babylonia) with
the capital at Babylon.




This was the period of our largest collection of Mathematical texts.
Nabu, god of writing and science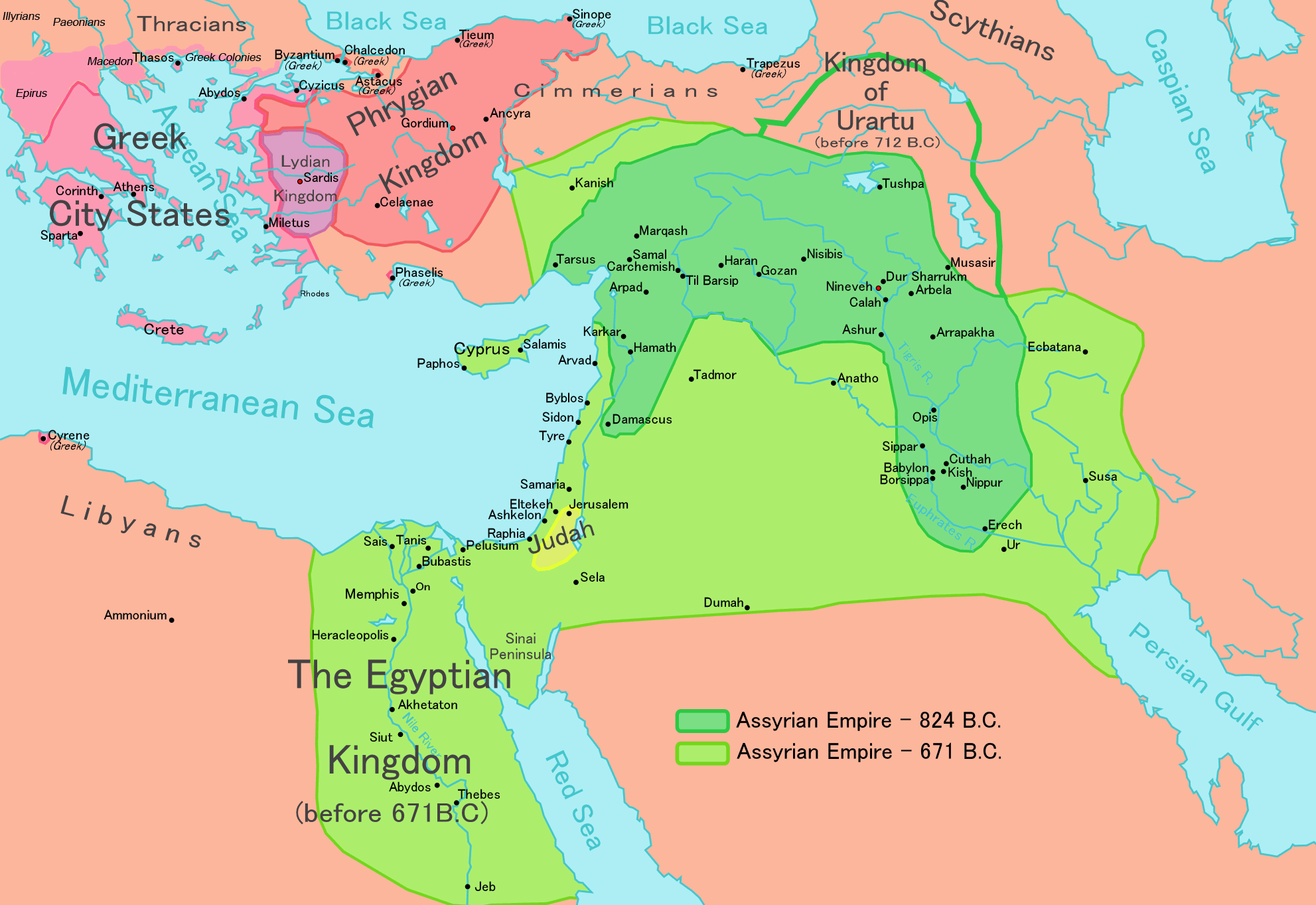
 The Assyrians spoke a dialect of Akkadian (like the Babylonians)
and, later, the Aramaic language.
No known mathematics. They are more known
for lion hunting
than scholarly pursuits.
The Assyrians spoke a dialect of Akkadian (like the Babylonians)
and, later, the Aramaic language.
No known mathematics. They are more known
for lion hunting
than scholarly pursuits.
Famous for human headed lions and bulls (protective dieties).
Winged bull.





Ninevah destroyed in 612 BC by an alliance (Medes, Chaldeans, etc.).
 Ishtar Gate built by
Nebuchadnezzar II (ca. 575).
Ishtar Gate built by
Nebuchadnezzar II (ca. 575).


Persians captured Babylon in 539 BC, putting an end, for the last time, to the Babylonian empire.
Before the modern discoveries, there were fascinating tales by
the Ancient Greek author Herodotus.
And much in the Bible.
Assyriology began at the shear
cliffs
of Behistun (Bisotun), Iran. 300 feet high.
Trilingual (all cuneiform)
inscription: Old Persian, Elamite, Akkadian.
It records the deed of the famous Persian king Darius (c. 520 BC).
Henry Rawlinson (1810-1895) an Englishman interested in Persian
antiquities first translated the Old Persian part (starting in 1837).
He an others translated the other parts (by 1857).
He and others risked lives to copy the writing from the cliff.




There are now a half-million tablets, with thousands mathematical.



Our knowledge of Babylonian mathematics dates from 1935.
The scholars Otto Neugebauer and
F. Thureau-Dangin are largely responsible for our knowledge.
There over a thousand mathematical tablets. About half are mathematical tables, and the rest are mathematical problems.
Example:
Multiplication by 9, multiplication by 7 and 1000.
Table of inverses (or reciprocals).



Example 1. When the area of a square is added to four times its width, a big unit (in other words 60) results. What square does this?
Solution. Square 2. Add this to the sum. Now you have 1, 4. Find the square root. This is 8. Now remove the 2. The answer is 6.
Example 2. The area is 7;30. The length and width add to 6; 30. Find the rectangle that does this.
Solution. Divide 6; 30 by 2. (This gives the average 3; 15). Square this to get 10; 33, 45. Subtract the area of the rectangle from this square, to get 3; 3, 45. Find the square root to get 1; 45. Add and subtract this from the average: answer 5 and 1; 30.
Example 3. How to see (a+b)2 = a2 + b2 + 2 ab geometrically.





 Here is a drawing, with translation, and related (recreated and speculative) quantities
Here is a drawing, with translation, and related (recreated and speculative) quantities


 For example, the first row describes a 119, 120, 169 triangle.
The first column (partly broken off) is
probably 1202 / 1692 (or 1; 59, 0, 15),
the second column is 119 (or 1, 59), and the third is 169 (or 2, 49).
There seems to be an error in the last row, which different
translators fix in different ways. According to one source
it describes a 28, 45, 53 triple. (The side 45 is not
explicitly written. The first column is 532 / 452
which is 1 ; 23, 13, 46, 40 (or 1.38716 ... in decimal). Other
sources describe it as a 56, 90, 106 triangle.
For example, the first row describes a 119, 120, 169 triangle.
The first column (partly broken off) is
probably 1202 / 1692 (or 1; 59, 0, 15),
the second column is 119 (or 1, 59), and the third is 169 (or 2, 49).
There seems to be an error in the last row, which different
translators fix in different ways. According to one source
it describes a 28, 45, 53 triple. (The side 45 is not
explicitly written. The first column is 532 / 452
which is 1 ; 23, 13, 46, 40 (or 1.38716 ... in decimal). Other
sources describe it as a 56, 90, 106 triangle.
Volume of boxes (rectangular parallelpipeds).
Truncated pyramid (frustrum), with a different formula
than the Egyptians.
Probably prisms and cyllinders given accurate area computations.
Similar triangles, Pythagorean theorem, even Thales' theorem.
(The text from Susa says that the perimeter of an inscribed hexagon divided by
the circumference is 0; 57, 36.
This fraction, in our notation, is 57/60 + 36/60^2 = 3456/3600 = 2^7 3^3 / 2^4 3^2 5^2
which simplifies to 24/25.
This leads to 25/8 for pi.)